Redback Aviation’s Helicopter Calculation Tools
ABOVE IMAGE: Courtesy http://www.tervis.fidisk.fi/JTsite/windtunnel.html
Helicopter Calculations
How much horsepower do you need to lift your homebuilt helicopter?
Approximately 12 pounds (maximum) gross weight per horsepower (at the rotor).
How much horsepower is required per square foot of main rotor disc area?
Approximately 4.5 to 5 square feet of rotor disc area per horsepower.
What length main rotor blades do you need to life your homebuilt helicopter?
Approximately 1.5 to 2.5 pounds (gross weight) per square foot of rotor disc area.
Below, we will demonstrate a method to calculate the theoretical thrust that that a propeller or rotor can generate. Of course in a helicopter, the rotor disk is oriented such that we call its force “lift” rather than thrust, “thrust” would be used in the case of an airplane. On a helicopter, the force of a tail rotor would be best described as thrust.
The first step is to measure the diameter of the rotor or propeller and calculate the area in square feet. Area is defined as:
A [ft^2] = Pi * r^2
-or-
A [ft^2] = (Pi/4) * D^2
where r is the radius of the propeller or rotor disk and D is the diameter in feet, of course Pi is the number 3.141592653589793238462643
If we know the area of the disk in square feet, we then need to know the amount of power that is delivered to the rotor. This needs to be in the units of horsepower. To convert the metric system of units Watts to horsepower, use the conversion: 1 horsepower = 745.699872 Watts. The goal is to calculate a parameter called “power loading” in units of horsepower per square foot. Power loading is calculated by:
PL [hp/ft^2] = power / A
Where “power” is the power delivered to the rotor or propeller and A is the area, calculated above. This is very important—approximately 10 to 15 % of the engine’s power will be delivered to the tail rotor to counteract torque. This number obvisouly varies but 10 to 15 percent is a good starting point. If you have a 100 horsepower engine in your helicopter, expect only 85 to 90 horsepower to actually get to the main rotor.
Additionally, you would need to reduce the power by an additional small percentage to account for frictional losses in the drive system. In the case of a tandem rotor helicopter such as the Chinook or meshed rotor like the Kmax, all of the power will be delivered to the main rotor and this in fact is the reason those helicopters are so well suited for heavy load lifting operations.
Using the parameter PL [hp/ft^2], we use an empiracly defined formula to calculate the thrust loading (after McCormick). Thrust loading is in the units of pound per horsepower and is a function of power and rotor disk area. Thrust loading (TL) is calculated:
TL [lb/hp]= 8.6859 * PL^(-0.3107)
Now that thrust loading is calculated, we can find the total thrust of the propeller (or lift of the rotor).
Lift = TL * power >>>[lb] = [lb/hp] * [hp]
*note: Calculation results are in pounds-thrust, NOT pounds-mass
Below are some common examples of the thrust developed by common aircraft engines and typical helicopters:
Theoretical thrust developed by common airplane engine – propeller combinations:
-
300 hp, 78″ propeller develops 1,300 pounds of thrust
-
80 hp, 50″ propeller develops 400 pounds of thrust
-
1.5 hp, 12″ propeller develops 10.5 pounds of thrust
Theoretical lift developed by common helicopters:
-
300 hp, 30′ rotor develops 3,400 pounds of lift (neglecting loss to tail rotor of 10-15%)
-
25 hp, 12′ rotor develops 347 pounds of lift (neglecting loss to tail rotor of 10-15%)
-
2 hp, 6′ rotor develops 39 pounds of lift (neglecting loss to tail rotor of 10-15%)
-
0.25 hp, 10.5″ tail-rotor develops 2.9 pounds of thrust
Full series of example calculations:
-
[EQ1]: PL [hp/ft^2] = power / A
-
[EQ2]: TL [lb/hp]= 8.6859 * PL^(-0.3107)
-
[EQ3]: Lift = TL * power >>>[lb] = [lb/hp] * [hp]
Using equation one, we calculate power loading (PL) of a 6 foot diameter (72″) disk with 300hp absorbed.
-
PL = 300 / (pi*3’^2)
-
PL = 300 / 28.27
-
PL = 10.61 hp/ft^2
Using equation two, we calculate the thrust loading. Typical communication/interpretation error is in the negative exponent of the equation. Remember, X^(-Y) is the same as 1/(X^Y).
-
TL = 8.6859 * (10.61^-.3107)
-
TL = 8.6859 / (10.61^.3107)
-
TL = 8.6859 / 2.083
-
TL = 4.2 [lb/hp]
Using equation three, we calculate the lift/thrust.
-
Lift = TL * power
-
Lift = 4.2 * 300
-
Lift = 1,251 pounds
Helicopter Weight and Balance Calculations
When determining whether a helicopter is properly loaded, two questions must be answered:
-
Is the gross weight less than or equal to the maximum allowable gross weight?
-
Is the CG within the allowable CG range, and will it stay within the allowable range throughout the duration of flight including all loading configurations that may be encountered?
To answer the first question, just add the weight of the items comprising the useful load (pilot, passengers, fuel, oil (if applicable) cargo, and baggage) to the basic empty weight of the helicopter. Ensure that the total weight does not exceed the maximum allowable gross weight.
To answer the second question, use CG or moment information from loading charts, tables, or graphs in the RFM. Then using one of the methods described below, calculate the loaded moment and/or loaded CG and verify that it falls within the allowable CG range shown in the RFM.
It is important to note that any weight and balance computation is only as accurate as the information provided. Therefore, ask passengers what they weigh and add a few pounds to account for the additional weight of clothing, especially during the winter months.
Baggage should be weighed on a scale, if practical. If a scale is not available, compute personal loading values according to each individual estimate. Figure 6-2 indicates the standard weights for specific operating fluids. The following terms are used when computing a helicopter’s balance.
| FIGURE 6.2 FLUID WEIGHTS | |
|---|---|
| Aviation Gasoline (AVGAS) | 6lb/gal |
| Jet Fuel (JP-4) | 6.5lb/gal |
| Jet Fuel (JP-5) | 6.8lb/gal |
| Reciprocating Engine Oil | 7.5lb/gal* |
| Turbine Engine Oil | Varies between 6 and 8lb/gal* |
| Water | 8.35lb/gal |
| *Oil weight is given in pounds per gallon while oil capacity is usually given in quarts; therefore, convert the amount of oil to gallons before calculating its weight. Remember, four quarts equal one gallon. | |
Figure 6-2. When making weight and balance computations, always use actual weights if they are available, especially if the helicopter is loaded near the weight and balance limits.
Helicopter Reference Datum
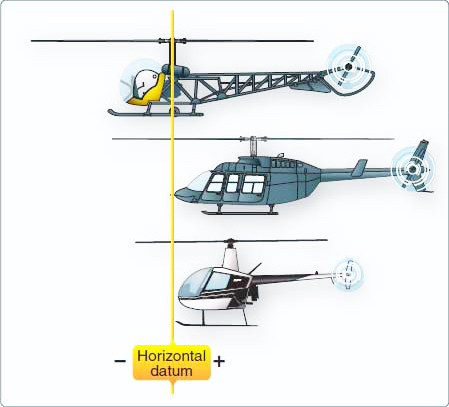
Balance is determined by the location of the CG, which is usually described as a given number of inches from the reference datum.
The horizontal reference datum is an imaginary vertical plane or point, arbitrarily fixed somewhere along the longitudinal axis of the helicopter, from which all horizontal distances are measured for weight and balance purposes.
There is no fixed rule for its location. It may be located at the rotor mast, the nose of the helicopter, or even at a point in space ahead of the helicopter. [Figure 6-3]
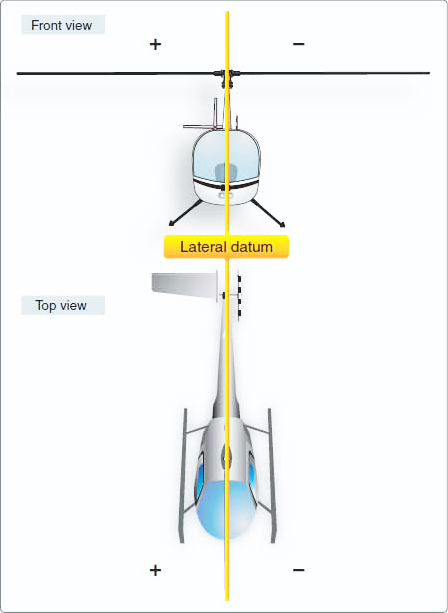
Figure 6-3. While the horizontal reference datum can be anywhere the manufacturer chooses, some manufacturers choose the datum line at or ahead of the most forward structural point on the helicopter, in which case all moments are positive.
This aids in simplifying calculations. Other manufacturers choose the datum line at some point in the middle of the helicopter in which case moments produced by weight in front of the datum are negative and moments produced by weight aft of the datum are positive.
The lateral reference datum is usually located at the center of the helicopter. The location of the reference datum is established by the manufacturer and is defined in the RFM. [Figure 6-4]
Figure 6-4. The lateral reference datum is located longitudinally through the center of the helicopter; therefore, there are positive and negative values.




Hi,
please, where can i download the coaxial helicopter calculator?
Thank you very much.
Best regards,
Aleksandar
All calculators are available for download at http://www.tervis.fidisk.fi/JTsite/index.html
Thanks
Please opinion installing a machine from Suzuki Hayabusa on a helicopter?
Thanks
Homemade helicopter weight 300kg, power plant 130hp rotor blades operating at 500rpm
How long(rotor blades)do they need be? 2 blade helicopter
How would RPM of the motor factor in to the equations? What RPM does this equation work for?