Helicopter Vibration Sources

With all the moving parts there is plenty of opportunity to develop vibrations. Surprisingly, not all high time helicopter pilots really understand these helicopter vibrations phenomena. One pilot reported, “If you have a 1/rev, the bird is out of track. If you have a 2/rev, it is out of balance”.
The gentleman undoubtedly has more vertical autorotation time that I will ever achieve in total hours. However, he didn’t have a clue about the vibration sources of the helicopter he was flying.
Even A&Ps as well as I/As can be found possessing very limited understanding of the sources of helicopter vibrations. However, as builder and maintainer of an experimental helicopter, you need to know more about the helicopter vibrations and their causes.
VIDEO: Out-of-balance “can” lead to ground resonance
Sources Of Vibrations In Helicopters
Engine Vibrations
The engine has a relatively high frequency: 45Hz (cycles/sec) for Lycoming, 83.3Hz for 5000 rpm engines, such as the Rotorway helicopters and some of the two stroke engine ships; 1000Hz for the turbine powered helicopters such as the Helicycle).
Tail Rotor Vibrations
The tail rotor rpm is the same as the engine rpm on the Safari and probably close for other choppers, except turbines and we know their tail rotor doesn’t spin at 60,000 rpm just because the engine does.
Main Rotor Vibrations
This is potentially the biggest source. If the thing wiggles, you know the whole ship will. The frequency is 8.33Hz for a 500 rpm two-blade ship at 1/rev.
NOTE: 1/rev is where you get one bump for every complete rotation of the rotor. Since the main rotor is the biggest source of shakes, it pays to take a look and see where some of these helicopter vibrations come from.

1/rev
Tracking & Helicopter Vibrations
For the most part, out of track blades give a 1/rev vertical vibration, caused by the tips of the blades not going through the same spot each rotation.
This is frequently a result of the pitch settings being different for each blade. Numerical measurement of 1/rev vibration is probably best sensed by the accelerometer mounted vertically as far forward of the e.g. as practical.
Tracking the blades, sometimes called “stick” tracking, with the ship on the ground at near hover, handles part of the tracking problem. But, forward flight speeds can show aerodynamic differences in the blades; possibly leading to a Climbing Blade.
Detecting which blade is doing the climbing is most easily accomplished with a strobe from the cockpit, using different color reflectors, positioned on each blade tip.
If red and green reflectors are used, when the pitch adjustments are made and the blades are tracking closely, an apparent single yellow reflector should be seen.
The correction of the Climbing Blade is usually done with trim tabs or trailing edge adjustments. However, a perfectly tracked blade does not always yield the smoothest flight.
Often when out of track blades make the ship smoother, this is compensating for some other condition. Out of balance blades. Both span wise and chordwise out of balance conditions most often cause a lateral 1/rev.
Both are readily solved by the judicious (judicious can be trial and error or a lot easier and quicker by the use of an electronic balancer) addition of weights attached to the blades for spanwise and to the rotor head for the chordwise.
Some people prefer to “sweep” the blade to compensate for out of balance chordwise conditions. While this works, it should be kept small and primarily involve just lagging one blade. Advancing a blade can cause vibration problems better avoided.
Swept blades, if swept excessively, can cause tracking errors in forward flight, which can show up as an increase in the vertical 1/rev while your lateral 1/rev will be reduced. On my ship, I keep the blades straight and added weights to the side of the yoke, Works for me.

2/rev
Here’s one that isn’t understood very well. In 2/rev vibration you get two bumps for every complete rotation of the blades. Since both lift and drag vary as the square of the velocity of the air, it seems appropriate to look at what the velocity of the air is where it hits the rotor blade.
The air velocity at a point on a hovering blade is:
V=Rs*R
– where
-
V is the air velocity caused by the blade rotation,
-
Rs is the rotor speed in radians/sec
-
R is the distance in feet from the center of the hub to the point in question.
So for a hovering helicopter in no wind, both the lift and drag forces are proportional to velocity squared, (you know this, right?) so:
V²= (Rs*R)2
However when forward flight is commenced, (or hovering in a non-zero wind) things change. The velocity of the air that impacts the same point on the blade has an additional term.
Vt=Rs*R+Vf*Sine(A)
– where
-
Vt is the total air velocity in ft/sec.
-
Vf is the forward speed in ft/sec.
-
Sine(A) is the Sine of angle A made between the span of the blade and the forward velocity.
Now, since the forces we are interested in are proportional to the velocity squared, then, (even at the risk of losing 50% of my readers), I will square the velocity and see what is in there.
Vt²=(Rs*R)²+2*(Rs*R)*Vf*Sin(A)+(Vf*Sin(A))²
This can be written as:
Vt²=(Rs*R)²+(Vf²)/2 +2*(Rs*R)*Vf*Sin(A)+(Vf²)*(cos(2*A))/2
Let’s take a look at what we’ve got:
First two terms: (Rs*R)² +(Vf²)/2 do not depend on the position of the blade and basically have no time variance. The lift and drag forces caused by this squared velocity will not generate any vibration. No 2/rev in a hover (Vf=0)
The third term: 2*(Rs*R)*Vf*Sin(A) depends on the angular position of the blade and has the time varying nature needed to produce vibration.
However, comparing the amplitude of this term to the last term and plugging in typical values for Rs, R and Vf, shows that this term is relatively negligible. Also, Shawn Coyle points out that the forces on the two blades are of opposite signs and cancel each other.
Basically this leaves our…
Vt²=(Rs*R)²+(Vf²)/2 +(Vf²)*(Cos(2*A))/2
Important!!! See this last term: (Vf²)*(Cos(2*A))/2?
This is the portion of the Vt² that is varying two times for every rotation of the blade!!!
The 2/rev forces are here! The Cos(2*A) provides the description of the two bumps per rotation of the blades that is needed to have the 2/rev vibration force.

Comparisons of the amplitude of the remaining terms show that while the 2/rev term is small to begin with, it increases with the square of the forward velocity.
These equations were solved in an Excel spread sheet for typical values of rotor speed, a position six feet out onto the blade and for forward velocities out to and including 90mph.
Basically the result is as follows:
-
It doesn’t matter if you are flying a Hiller, Bell Jet Ranger, Helicycle, Safari, Rotorway or? If it is a two-blade helicopter in forward flight, there is both a drag and lift force varying at twice the rate of the rotor speed!! E.g. 2/rev.
-
The math agrees with experience, e.g there are no forces varying with 2/rev in a hover.
-
The force varying with 1/rev (on a tracked and balanced rotor system) generated in forward flight, while it exists, is much smaller than the 2/rev and is for all practical purposes, negligible. (Shawn Coyle says it cancels. My measurements, while indicating a slight increase in vertical 1/rev with increased forward velocity, tend to agree with Shawn).
-
Those lift and drag terms, not varying with blade position as a function of time, do increase with increasing forward speed. No surprise here.
-
The magnitude of the 2/rev term is much smaller than the non-time varying portions of the generated force, but also increases with the square of the forward speed.
-
You can’t get rid of the 2/rev forces in helicopter vibrations. They are part of the process whereby your lift is generated.
-
2/rev vibrations felt in the fuselage are due to some element of the fuselage resonating with the input forces as calculated above. These forces can shake your ship.
Note: This 2/rev derivation focused only on the forward velocity derived forces. Other sources are there also. One can be experienced when the cyclic is displaced on ground run-up, while the rotor disc is displaced from perpendicular to the mast — there is no forward velocity at this time.
What you do with this is another question?
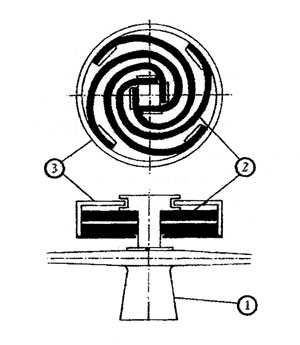
Westland flexispring vibration absorber.
If you can develop an opposing force of roughly the same magnitude and opposite phase, the vibrations can be effectively cancelled. This would be an active cancellation of helicopter vibrations, typically involving a computer and expensive to develop.
There have been numerous non-active methods derived to stop these vibration sources from shaking the pilot and wearing out the controls. An interesting one was the Westland developed flexispring vibration absorber (shown in the picture below), using a spring-mounted ring attached to the rotor mast.
The theory being the vibrations from the blades would shake this device, which would respond and provide a canceling vibration, out of phase with the shake coming from the blades.

Fludilastic Pylon Strut
Weight of the unit for a 10,000 lb helicopter was said to be 120 lb. Can this be linearly scaled down to a 1500 lb ship? Another interesting passive cancellation being investigated is a “Fluidlastic” dampener, mounted in the pylons and supporting the mast.
This uses liquid to produce the effect of a high static spring constant with a much lower dynamic spring constant. Sound impossible? Turns out, the concept has been around for awhile and has a history of being able to provide some serious reductions in vibrations felt in the pilot’s seat.
As a side note a gentleman who has written papers on this subject, Dennis McGuire, was at Homer Bell’s this year looking at some of the helicopters and has promised to investigate a possible Fluidlastic damper design, scaled for use on our two blade helicopters.




Hi from Jim in Madras oregon. 2 items.
1. the right mouse click functions don’t seem to work, ie; open link in a new tab.
2. I wasn’t able to seen a message via the comtact us page. it just keeps saying there is a problem, try again later.
3.i appericate the redesigned web site and all thework that has gone into it. It will take me months to read it all.
4. do you know of anyone currently flying a lone star in the states? particularly intrested in the west coast. or anyone that has one. I think this is my chosen bird and want firsthand current info.
Tks again for all you do. I don’t paypal but would like to help with funding. Jim
Hi Jim, sorry for taking so long to reply. We have gone over your comments and fixed these problems. Thank you for making us aware of these important issues.
1. Turned off right click security block – you can now right click
2. Fixed errors on the email form settings – you can now email
3. Thank you, I will add to the website more regularly which hopefully means endless reading?
4. In the past, I had heard of only 3 flying craft – one was in Japan, one in the north east USA and one on the west coast USA. I have no details or contacts for any of these but invite people to submit and set-up a owners list.
I appreciate you wanting to help with the website funding – but only use PayPal as it offers both parties the security they are entitled to. Just as a footnote – you can make one-off payments using a credit card through PayPal without signing up – though they do make this system hard to understand and complete as they would prefer user memberships to increase their bottom line.
Kind regards,
Adam